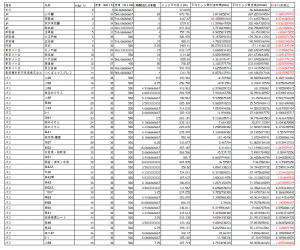
This example is about Tokyo Ueno area.
都市には坂道などの要素以外にも,鉄道網やバス網といった交通手段があり,私たちはこれらを利用しながら日々活動しています。徒歩以外の移動手段を考えて都市をはかるには,徒歩に対してどの程度速度が速く,また距離を縮めているかを計算することが効果的です。この考えを基にした「時間変形地図」を描くことで,異なる速度を有する交通網がどのように都市空間を変形しているかを見ます。
本ポストの動画は、出発点から目的地点までの最短経路を探索し、その経路上を「時間変形地図」を描きながら移動していく様子です。
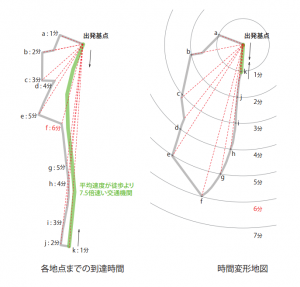
時間変形地図の描き方
Step 1. まず出発基点を決め,他のすべての地点までの(最短)到達時間を計算します。
Step 2. つぎに出発基点を中心として等間隔(左図では1分刻み)の同心円を描きます。
Step 3. そして,出発地点から他のすべての地点までの角度を保ったまま,到達時間に応じて各地点を移動させると時間変形地図が描けます 。
見なし距離を縮める装置としての交通網図
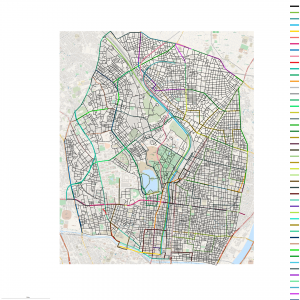
(c) OpenStreetMap contributors, CC-BY-SA
この上野エリアには、徒歩街路の他に14路線の鉄道網と33路線のバス網が運営されています。基点から各地点まで,最短時間で到着できる経路を選び,見なし距離を計算して地図を描いています。
交通機関を利用して移動速度を速めたため,遠くの地点の到達時間が早まり,見なし距離が縮まって,現在基点に近づいた(引き寄せられた)と見えます。時間を主題にして描いた地図です。各交通網が,現在基点に向かって街路を引き寄せている様子が見られます。都市空間において,交通機関は,地理的制約を越えて,見なし距離を短くすることのできる機械装置のようなものに見えてきます。
待ち時間を考慮する
しかし現実的には,徒歩との速度比によってだけで交通網の見なし距離を算定するのは適切ではありません。例えば徒歩の平均時速を4km,バスの平均時速を30kmとすると,バスの見なし距離は徒歩の約1/7.5となります(図2)。しかし実際にバスを利用する場合,まずバス停まで向かい,バスが来るのを待って路線に乗ります。すぐに乗れることもあれば,次のバスまで待つこともあり,すぐに乗れるほど,時間は稼げ,見なし距離も短くすることができると考えられます。
厳密には,時間変形地図は時々刻々と変化することになりますが,ここでは,バスの運行本数から平均的な待ち時間を算出し,鉄道やバスの徒歩速度に対する平均速度を計算しました。 すると,33のバス路線のうち,じつは5路線を除いては,徒歩で移動したほうが速く(バスを利用する動機にならないともいえます),地図が変形しないことがわかりました。
このとき,大体の目安として,バス停間の平均距離が300m程度と短いと毎時8本以上,700m程度と長い場合でも毎時5本以上の運行がされていれば,バス停間の見なし距離が縮まることが割り出せました。
都市のハードウェア・ソフトウェア オペレーション
交通機関を計画・運営するということは,機械装置によって見なし距離を人工的に調整して都市を図る行為,ともいえるでしょう。鉄道では,どこに新たな路線を敷設するかどの地点(駅)を結ぶか,というハードウェア計画によって,またバスでは路線の経路計画,運行時間帯,本数といった運営方法というソフトウェアによって,見なし距離が計られているのです。時間変形地図は都市を利用する私たちにとっての,都市の広さをはかり,利便性を示す方法の一つといえます。